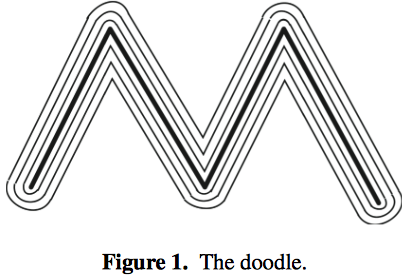
A fearful sphere, whose center is everywhere
In a beautiful article, The Mathematics of Doodling, Ravi Vakil poses two problems:
- Given a random curve, like a doodle, in what sense do closed curves successively drawn around the doodle become more and more circular?
- How do geometric invariants, like area and volume, of the closed curves relate with the original shape and with each other?
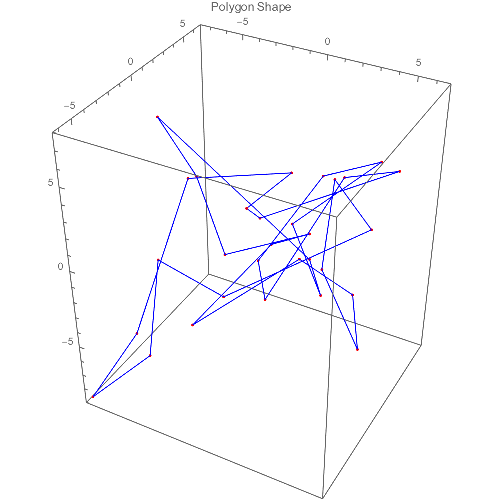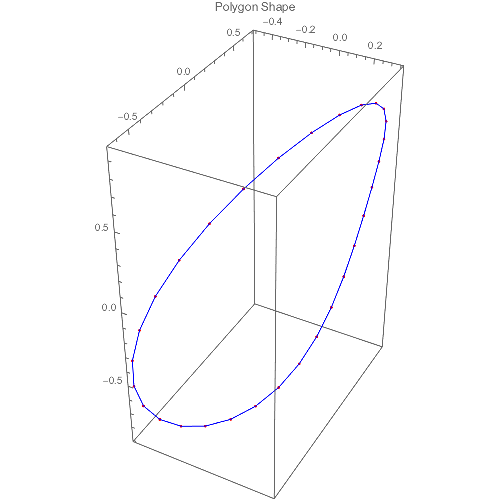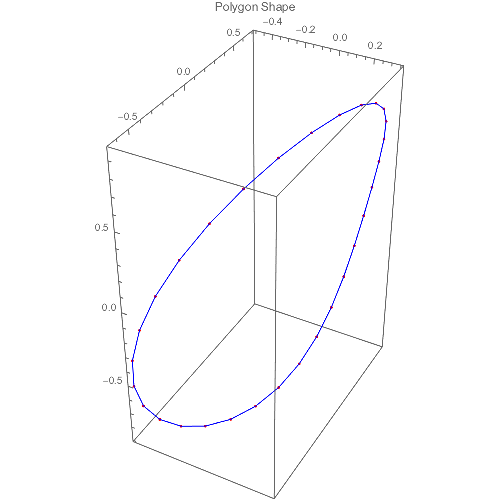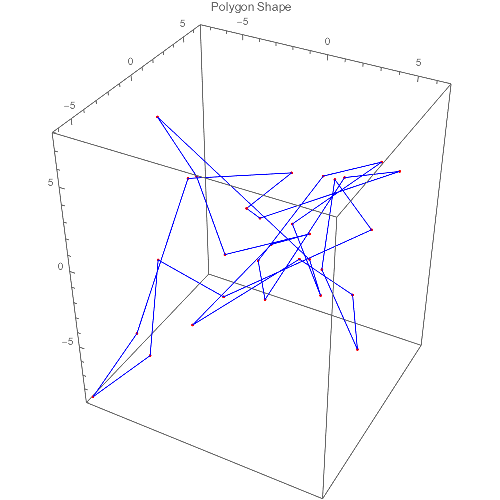
The first question, at least, seemed connected to another interesting paper, Random polygon to ellipse: an eigenanalysis. Here Elmachtoub and van Loan ask:
- If we start with a random polygon and then create a succession of polygons by averaging the vertices of the previous polygon, do the polygons converge to something structured?
- How is this structure related to the initial configuration of the polygon?

One uses geometry, and the other uses matrix analysis to investigate these question but both seems to ask how certain iterations of a geometric body lead to another.
Let’s pose two related problems, and explore two methods that may give insight:
- What kind of iterations transform bounded convex polyhedra to a circle?
- How are the centroids of the polyhedra related to the center of the circle?
Cimmino’s algorithm
Gianfranco Cimmino [Benzi04] gave a unique method for solving a system of linear equations (A . x = b **i.e. **ai . x = b, i = 1, 2…m). To find the point of intersection of m n-dimensional hyperplanes:
- start with an arbitrary point y
- find the mirror image of y with respect to each hyperplane to yield m projected points
- calculate a weighted centroid of these m points
- use the centroid as the new iterate
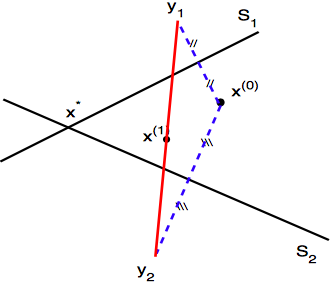
Cimmino iteration [ref][/caption]How do we find the mirror image? Given a hyperplane ai, its unit normal vector is - ai **/ **|a|, where || denotes the Euclidean norm. The distance between y and ai is ai . y - b, hence the distance between y and its reflection must be twice that. The unit normal vector transports y over a distance 2 (ai . y - b) to y + 2 (b - **ai .** y ) **ai **/ |a|**. Note that we need to choose the negative unit normal vector, instead of positive, to reflect the point around the hyperplane.
The centroid is the average of these reflected point: 2/m ∑ (b - **ai . y ) **ai **/ |a|**. The weighted centroid for arbitrary normalized weights wi would be: 2 ∑ wi** (b - **ai .** y ) **ai **/ |a|,** where ∑wi = 1.
In fact, this weighted centroid is only an approximation to the true geometric centroid of the polygon since the entire mass of the initial polygon isn’t concentrated in its vertices (otherwise, a single iteration would suffice). Successive iterations improve this approximation by shrinking the polygon to a point, which is the geometric centroid.
Censor and Elving extend Cimmino’s algorithm to a system of linear inequalities (Ax <= B) to fin one solution (i.e. a feasible point) [Censor83]. The calculation of the weighted centroid was all they needed to revamp, so the geometry of the algorithm remains unchanged. To prove convergence, the authors appeal to the Fejér montonicity [Combettes00] of iterates (cf. with contraction mapping for Banach space). A sufficient condition for convergence in their scheme is that wi > 0.
How does this relate to [Elmachtoub07]?
- In both Cimmino’s algorithm and [Elmachtoub07]’s Algorithm 1, the centroid is fixed but unknown. They both construct successive polytopes that converge to the centroid.
- Both Cimmino’s algorithm and Algorithm 1 converge to the centroid of the initial polygon.
- Cimmino’s polygon, far from being random, is specifically constructed using orthogonal projections of a given point. The constructed polygon is cyclic, and its circumcenter and centroid coincide.
- How do normalized iterates affect convergence? If iterates in Cimmino’s algorithm are normalized such that the circumcenter doesn’t change, then they oscillate on a limit cycle.
von Neumann’s algorithm
An early algorithm for solving a system of linear inequalities, A . x <= b, comes from John von Neumann via George Dantzig [Dantzig92].
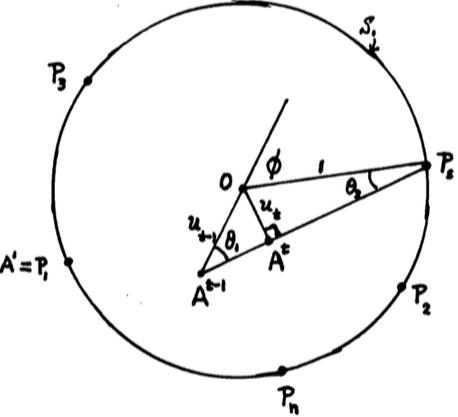
We start with a “standardized” polyhedron:
- Transform A . x <= b into ∑ Pj . x = 0, ∑ x = 1, x >= 0 such that |Pj| = 1. Thus the points Pj lie on a hypersphere of radius 1 and center 0.
- Select an arbitrary initial point x >= 0, such that ∑x = 1. This also corresponds to selecting an arbitrary point P1 on the hyper-sphere and considered as iterate A1.
- The aim is to set the next iterate At so that the distance, ut, to origin is minimized. This is done by choosing the hypersphere point, Ps, that minimizes the angle, φ, subtended by At-1 and Ps. Then At is point on the line At-1 - Ps and its normal that passes through origin.
- Iterate till ut decreases to ε.
Unlike Cimmino or Algorithm 1, the centroid is fixed and known as the circumcenter of given points. What the algorithm discovers, while solving the feasibility problem, is the polygon whose weighted point-mass centroid would be this circumcenter. Note that since the algorithm projects points to minimize distance to the center, the number of iterations is independent of the dimensions of the problem (unlike Cimmino). If iterates are normalized, then they are always projected on to the hypersphere, which would be their limit cycle.
Fourier polygons
Why does a general polygon, under averaging iterations, converge to an ellipse and not to a circle? The short answer is that the affine transformation of a circle is an ellipse.
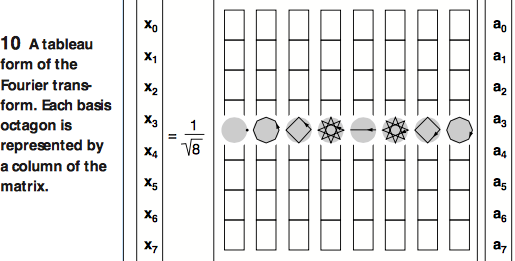
A compelling reinterpretation of the discrete Fourier transform [Glassner99] argues that the transform matrix can be viewed as regular polygons in the complex plane. As a corollary, any polygon can be decomposed into a weighted sum (an affine transformation) of regular polygons.
P=1nn−1∑k=0XkPk
In any such transformation, three regular polygons are important: P0, P1, and Pn−1. P0 corresponds on a point, but the other two are regular, convex n-gons. The averaging transformation can now be applied to this sum of regular polygons. As David Radcliffe argues, all component polygons shrink (except for P0) but P1 and Pn−1 shrink at the slowest rate leaving us with an affine combination of the three shrunk regular polygons converging to an ellipse. While [Elmachtoub07] uses a rather involved matrix analysis to converge a random polygon to an ellipse, Radcliffe’s argument is far more intuitive (and not too far from quantization).
Steiner, Weyl, Minkowski
We return to Vakil’s problem. For parallel bodies drawn around a non-empty convex body, K, Steiner proposed a volume formula:
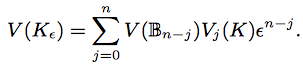
The formula, as Vakil notes, is polynomial in the radius, ε, of the neighborhood, and relates volume to surface area. Depending on ε, the volume may converge to an n-sphere, V(Βn), or to the volume of the convex body, V(K).
Notes
A fearful sphere comes from a handful of metaphors. For linear systems, Kaczmarz and Cimmino are basic iterative algorithms, now considered part of projection methods. von Neumann studied the general question - maps of linear operators - of early on. The discrete Fourier transform can be viewed geometrically and applied to geometric shapes. The Steiner formula is a special instance of Minkowski’s mixed volume [Schröder08], and Weyl’s formula for the volume of a tube of a submanifold.
Fourier polygons
- Benzi04 M. Benzi. Gianfranco Cimmino’s contributions to numerical mathematics.
- Combettes00 P. Combettes. Fejér monotonicity in convex optimization.
- Censor83 Y. Censor, T. Elfving. New methods for linear inequalities.
- Dantzig92 G. Dantzig. An ε-precise feasible solution to a linear program with a convexity constraint in 1/ε² iterations independent of problem size.
- Elmachtoub07 A. Elmachtoub, C. van Loan. Random polygons to ellipse: an eigenanalysis.
- Glassner99 A. Glassner. Fourier polygons.
- Shröder08 P. Schröder. What can we measure?
- Vakil04 R. Vakil. The mathematics of doodling. .