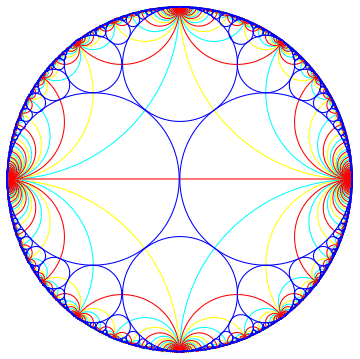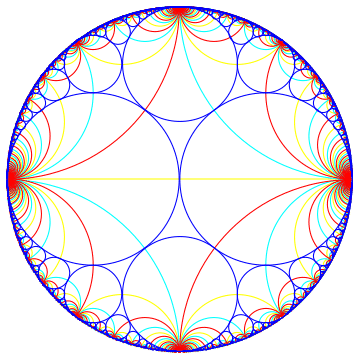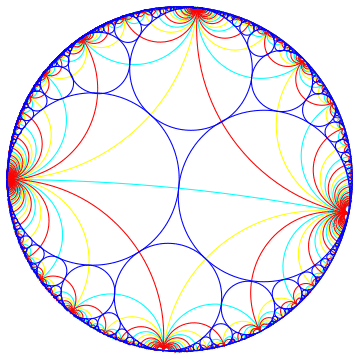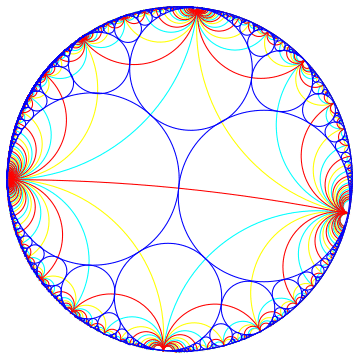
Farey tessellation in complex plane.

In fact, the matrix formulation of Fibonacci numbers mentioned before can be generalized to represent any 2-D matrix and, by way of continued fractions, any real number - not just the golden mean. This post is inspired from David Austin’s AMS feature column and draws on Phillipe Flajolet’s beautiful survey on continued fractions to set the stage for a future post on Diophantine approximation.

“Every matrix A of determinant one with non-negative integer coefficients will have a unique factorization… corresponding to a continued fraction expansion.” [1]

A=[ab cd]=Uα0Lα1Uα2Lα3…whereU=[11 01],L=[10 11],andbd=a0+1a1+1a2+1a3+⋯

The Fibonacci numbers can be derived as

[latex]\left[ Fn−1FnFn−2Fn−1

\right] = ULULUL… \\ \phi(n) = \frac{F_{n}}{F_{n-1}} = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \dotsb}}}[/latex]

Of course, both the factorization series and the fraction terminate for finite values of n i.e. rational approximations of the golden mean. Already this formulation can be used to calculate the n-th Fibonacci number in log(n) steps.

While “every positive rational number appears in the Stern-Brocot tree,” [2] such factorization also represents a specific path in the tree whose nodes provide the optimal rational approximation to a real number within a given error.

References

• [1] P. Flajolet, B. Vallee, and I. Vardi. Continued fractions from Euclid to present day. Preprint, March 2000.
• [2] D. Austin. Trees, Teeth, and Time: The mathematics of clock making. AMS Feature Column, December 2008.