Optimization, particularly deterministic (convex) optimization, is essential to many learning algorithms (regression, support vector machines, matrix factorization etc). This post discusses first-order/gradient-based optimization approaches that may be more suitable for stochastic problems.

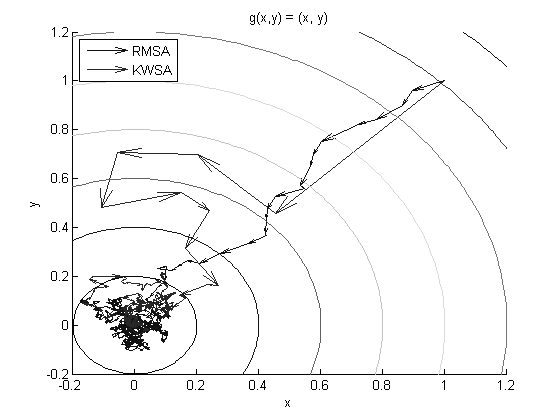
Robbins-Munro algorithm: stochastic gradient root-finding

• Assumptions, convergence rate
• The original algorithm assumes that the dimension of input and output are the same. This does’t work for overdetermined systems such as those in least-squares linear regression. Maeda-Kanata extend RM to handle the case where output dimension is greater than input.

Kiefer-Wolfowitz algorithm: finite differences instead of gradients

Polyak-Juditsy averaging: accelerating stochastic approximation

References

• PL. Pat Laub. Stochastic Root Finding Review
• [Borkar08] V. S. Borkar. Stochastic Approximation - A Dynamical Systems Viewpoint. Cambridge University Press, 2008.
• Bottou98 Online Learning and Stochastic Approximation. Online Learning and Neural Networks, ed. D. Saad, Cambridge University Press, 1998.
• CastleLab W. B. Powell. Computational Stochastic Optimization. Course Notes.
• Chen99 H. F. Chen, T. E. Duncan, and B. Pasik-Duncan. A Kiefer–Wolfowitz Algorithm with Randomized Differences. IEEE Transactions on Automatic Control, Vol. 44, No. 3, March 1999.
• Hill05 S. D. Hill. Discrete Stochastic Approximation with Application to Resource Allocation. Johns Hopkins APL Technical Digest, Vol. 26, No. 1, 2005.
• [Kushner98] H. J. Kushner and G. G. Yin. Stochastic Approximation Algorithms and Applications. Springer-Verlag, 1998.
• Kiefer52 J. Kiefer, and J. Wolfowitz. Stochastic Estimation of the Maximum of a Regression Function. The Annals of Mathematical Statistics, 1952.
• Klein07 S. Klein, M. Staring, and J. P. W. Pluim. Evaluation of Optimization Methods for Nonrigid Medical Image Registration Using Mutual Information and B-Splines. IEEE Transactions on Image Processing, Vol. 16, No. 12, December 2007.
• Kushner08 H. J. Kushner. Stochastic Approximation: A Survey, Nov. 2008.
• Maeda94 Y. Maeda, and Y. Kanata. Extended Adaptive Robbins-Munro Procedure Using Simultaneous Perturbation for a Least-Square Approximation Problem. Proceedings of the Asian Control Conference, July 1994.
• Maryak97 J. L. Maryak. Some Guidelines for Using Iterate Averaging in Stochastic Approximation. Conference on Decision and Control, December 1997.
• Mokkadem07 A. Mokkadem, and Mariane Pelletier. A Companion for the Kiefer-Wolfowitz-Blum Stochastic Approximation Algorithm. The Annals of Statistics, Vol. 35. No. 4, 2007.
• Munro51 H. Robbins, and S. Monro. A Stochastic Approximation Method. The Annals of Mathematical Statistics, 1951.
• Nemirovski09 A. Nemirovski, A. Juditsky, G. Lan, A. Shapiro. Robust Stochastic Approximation Approach to Stochastic Programming. SIAM Journal on Optimization, 2009.
• Polyak92 B. T. Polyak, and A. B. Juditsky. Acceleration of Stochastic Approximation By Averaging. SIAM Journal of Control and Optimization, Vol. 30, No. 4, July 1992.
• Shalizi C. R. Shalizi. Stochastic Approximation Algorithms. Notes, 2010.
• Shimkin11 N. Shimkim. The Stochastic Approximation Algorithm. Lecture Notes, Learning in Complex Systems, 2011.
• Zhang13 L. Zhang, T. Yang, R. Jin, and X. He. O(logT) Projections for Stochastic Optimization of Smooth and Strongly Convex Functions. Journal of Machine Learning Research, Vol. 28, 2013.